How do you find the equation of an ellipse? Or how do you calculate the equation of an ellipse? Or how do you find the formula for an ellipse? If you’re looking to answer any of these questions, then you’ve come to the right place! We’ve written this article to help you solve any issues you may have with calculating the equation of an ellipse.
What Is the Formula for an Ellipse?
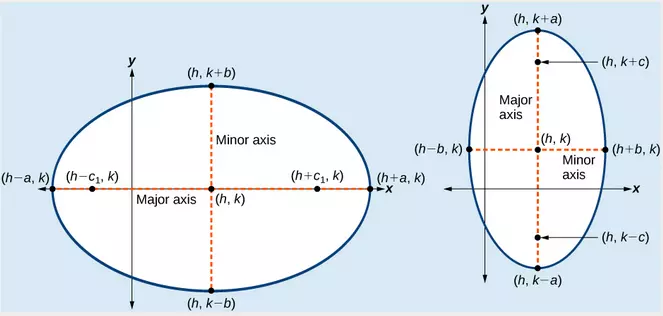
The equation of an ellipse calculator is a tool that helps you determine the mathematical formula for this type of curve. An ellipse is a closed curve that resembles a flattened circle. It’s made up of two points, called foci (or singular: focus), and the sum of the distances from any point on the ellipse to each focus is always constant. The equation of an ellipse can be written in several different forms, depending on how you want to use it. The most common form is the standard form, which is simply x2 = Ly+ Lz . To graph an equation of an ellipse using our equation of ellipse calculator’s, enter the values for your given lengths into our equation and click graph. If one value is entered into our equation of ellipse calculator, then there will only be one point on the graph. The results will give you a graphical representation of your equation with the major and minor axes drawn as well as any intersections with other equations or lines.
The equation of an ellipse can also be expressed in parametric form. Parametric equations are equations that describe all points along a specific parameter on an ellipse, such as its axis. These are created by specifying both variables on either side of the equation and their rate of change. For example, if you wanted to show points with coordinates (x1, y1) and (x2, y2) along the equation x=5t+4 for parameters t=0 through 2π, the equation would be written in parametric form as follows: 5(t)+4y=(x1-x2)+(y1-y2). When we enter these numbers into our equation of ellipse calculator’s in order to graph them out we’ll get a visual representation of these coordinates including intersection points with other equations or lines.
What Should I Put Into the Equation of an Ellipse Calculator?
There are a few key things you’ll need in order to calculate the equation of an ellipse. You’ll need the length of the semi-major and semi-minor axes, as well as the coordinates of the center point. Additionally, you’ll need to know either two points on the ellipse or one point or the eccentricity. With all of this information, you can plug it into an equation of ellipse calculator and get your answer! For example, if I knew that my equation of an ellipse had these three pieces of information: 2 for the length of the semi-major axis, 0 for the length of the semi-minor axis, and 2 for my center point’s coordinates, then I would plug those numbers into my equation of ellipse calculator’s. Once I did that, I would see that my equation is A=5*B^2+C*D+E. If you’re still not sure how to solve the equation of an ellipse, don’t worry! My equation of ellipses calculator will take care of everything for you!
You’ll need just five simple steps with our equation of ellipses calculator:
1) Plug in all your required variables (e.g., B for semi major axis, C for semi minor axis, D for center coordinates).
2) Choose between solving for points or eccentricity.
3) Decide what type of equation you want: standard form, standard form inverted, slant height, or slant height inverted.
4) Click solve to find your answer.
5) You can also use our equation of ellipse calculator’s graphing function by clicking graph.
Also Read: How to Use the Free Fall Calculator Check The All Details Here
The Formula for Any Circle
The equation of a circle is (x-h)^2 + (y-k)^2 = r^2. The h and k represent the coordinates of the center of the circle, and r is the radius. To find the equation of a circle when you only have its circumference, use this formula: C=2*pi*r. Plug in your numbers and solve for r. Once you have the radius, plug it into the original equation and solve for h and k. The ellipse will then be defined by x+i*2/a+j*2/b=1 and y+i*1/a+j*1/b=1 where i is ƒ(x), j is ƒ(y), ƒ(x)=e^(-4πix)/4, ƒ(y)=e^(-4πiy)/4. If a or b are equal to zero, they can be omitted from the equation. For example, if a=0, the equation would become x+i*2/0+j*2/0=1 and y+i*1/0+j*1/0=1.
A hyperbola will always have two sets of asymptotes that are perpendicular to each other on either side of the graph. Both lines intersect at the origin and slope towards infinity on either side. Asymptote one looks like a parabola that has been cut off, while asymptote two looks like a line with no visible curvature. Lines parallel to the axes are called transverse lines. Transverse lines intersecting with the curve near the origin form four angles known as gores. These are designated by their relation to the angle in degrees that is made with the horizontal axis. Lowercase letters refer to angles made below the horizontal axis; uppercase letters refer to angles made above it.
How Do I Graph My Points on a Coordinate Plane to Create an Ellipse?
If you’re looking for an equation of ellipse calculator’s, you’re in luck! There are a few different ways to calculate the equation of an ellipse, but we’ll focus on graphing points on a coordinate plane. To do this, you’ll need at least four points that lie on the ellipse. Once you have your points, you can use a graphing calculator or online graphing tool to graph them. Then, you can use the slope formula to find the equation of your ellipse.
A Quick Alternative Way to Calculate the Points on Your Plotting Chart
If you don’t want to use the ellipse equation calculator, there’s a quick alternative way to calculate the points on your plotting chart. First, draw a horizontal line through the center of your ellipse. Then, draw a vertical line perpendicular to the horizontal line at any point on the ellipse. The intersection of these two lines will be one of the points on your ellipse. First, draw a horizontal line through the center of your ellipse. Then, draw a vertical line perpendicular to the horizontal line at any point on the ellipse. The intersection of these two lines will be one of the points on your ellipse.