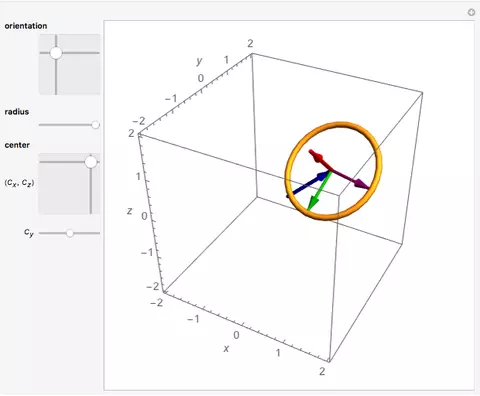
A parametric equation calculator 3D, also called curve plotter is an online tool that lets you graph parametric equations online and create animated 3D graphs of parametric functions. Here’s how to use it to visualize the parametric curves and surfaces you want to see. The first step to using this tool is determining whether you want to generate parametric equations or parametric surfaces; each generates its own kind of graph.
Introduction
Let’s say you have x, y, and z variables—and a function of x and y, like f(x,y) = 2xy. What if you want to plot f(x,y) for different values of y? To do that, it’s best to convert your equations into parametric form. In parametric form (also called t-variables or t-coordinates), both x and y are replaced with t. (In standard coordinates, only one variable is replaced with t. The other is the independent variable.) The third dimension (z) can be left out of the equation entirely, or else the equation would need to be rewritten as ƒ(t,t). In this example:
Parametric equation calculator 3d Curve plotter tutorial – Find how to use parametric equation calculator 3d curve plotter in details. It has many options for drawing such as line curve, step curve, spline curve etc.
Parametric Equations – Definition
A parametric equation for a curve is an equation in which two or more of the variables are expressed as functions of one other variable. The two most common forms of parametric equations are: ƒ(t) = (x(t), y(t)) and x = f(t). Both forms lead to infinite families of curves. For example, take ƒ(t) = (x, y) and let t range from 0 to 10. The resulting curve is an ellipse whose width increases as t increases. The curve also rotates counterclockwise around the origin with each value t. (See image below.) ## ## Graphing + Parametric eq formulae ## Take the function ƒ(t) = (x, y) where t ranges from 0 to 10. The resulting curve is an ellipse whose width increases as t increases. The curve also rotates counterclockwise around the origin with each value t. From these graphs we can see that when t=0 the coordinates x=0 and y=0. When t=10, the coordinates x=-5 and y=-5. Notice that when t=-2 then both coordinates are negative numbers.
Likewise, when t=4 then both coordinates are positive numbers. The graph will always rotate in the same direction regardless of whether the coordinate is positive or negative. As you can see from this parametric equation calculator 3d allow us to create shapes with infinitely many solutions while only providing one initial point? By changing just one parameter, such as t in our equation above, we can have different dimensions and directions. In addition to our parametric graph on the screen, there are four plots below it showing how certain parametric equations look depending on what t is. We’ve shown you a few examples but if you would like to see some others feel free to explore by clicking on Show More.
Parametric equations can be plotted using a graph
Plot with known parameters over x and y (x1, y1) vs. x and y (x2, y2). This is plotted by use of parabola equations found using either graphing calculator or Sphere Equation Calculator. A single equation can be used for both parametric equations: XY=c and YX=c where c = Constance. In this example, XY=6+Constance and YX=Constance are the two equations. These are then plotted on a graph as the abscissa and ordinate respectively; the X axis will give values in steps of h which represent units in the horizontal direction on a graph while the Y axis will give values in steps of k which represent units in the vertical direction on a graph. The curve generated from these points is then defined by an intersection point(s), which has coordinates (h0, k0), as shown below. When there is only one parameterized equation (e.g., XY=6+Constance), the curve follows a straight line between points that correspond to each of the constants along it.
When there are two parameterized equations, such as XY=(2-k)+5*k and YX=(-5*k)-10*k, that intersect at point P with coordinates (-8,-4), we find its value by substituting -8 for h and -4 for k into one of our equations and solving it for t:
t=-8/(5*(-4))=-32<0 so this equation does not generate any values between 0≤t≤30 because when h>0 and k>0, the slope m=slope(k, h)=20 > slope of either 6+(2-k) or 5*(k-10), which are equal to m=14. On a graph showing parametric curves with their equations plotted as abscissa and ordinates respectively, a parabolic shape is seen.
There exist many interesting applications for 3d plotting capability offered by online math calculators:
Parametric curves plotting can also be done in three dimensions rather than just two dimensions! To do this, you plot all the parametric points (x1, y1, z1) versus x2 and y2 on a graph. To do this we need two equations: XYZ=c and YZX=c where c = Constance. We need to calculate all the z coordinate values before moving onto plotting them on the graph. The first step is to solve for z using whichever equation you want first – note that if you solve for Z first your Z axis range will be . Then plug in those results into your other equation and solve again – now we have all four variables solved!
Calculating the coordinates of points on the curves
Parametric equations are essential for many fields of study such as electrical engineering, design and other fields where scientists and engineers use different formulas to solve problems. These formulas plot three-dimensional curves that can be used for various purposes. To calculate coordinates of points on these curves, you have to multiply any point on your curve by a t parameter. The t parameter is equal to time in seconds. You may also need to apply some trigonometric functions. These functions include cosine, sine and tangent among others. When it comes to parametric equation calculator 3d, the xy plane is divided into four quadrants. The x axis goes from negative numbers up to positive numbers while the y axis ranges from negative numbers down to positive numbers. Every quadrant has its own set of at values with two dimensions corresponding to the height and width values. In order to make calculations easier when using parametric equations, it’s important not only to understand how they work but also know how they’re constructed mathematically so you’ll have an easier time manipulating them later on.