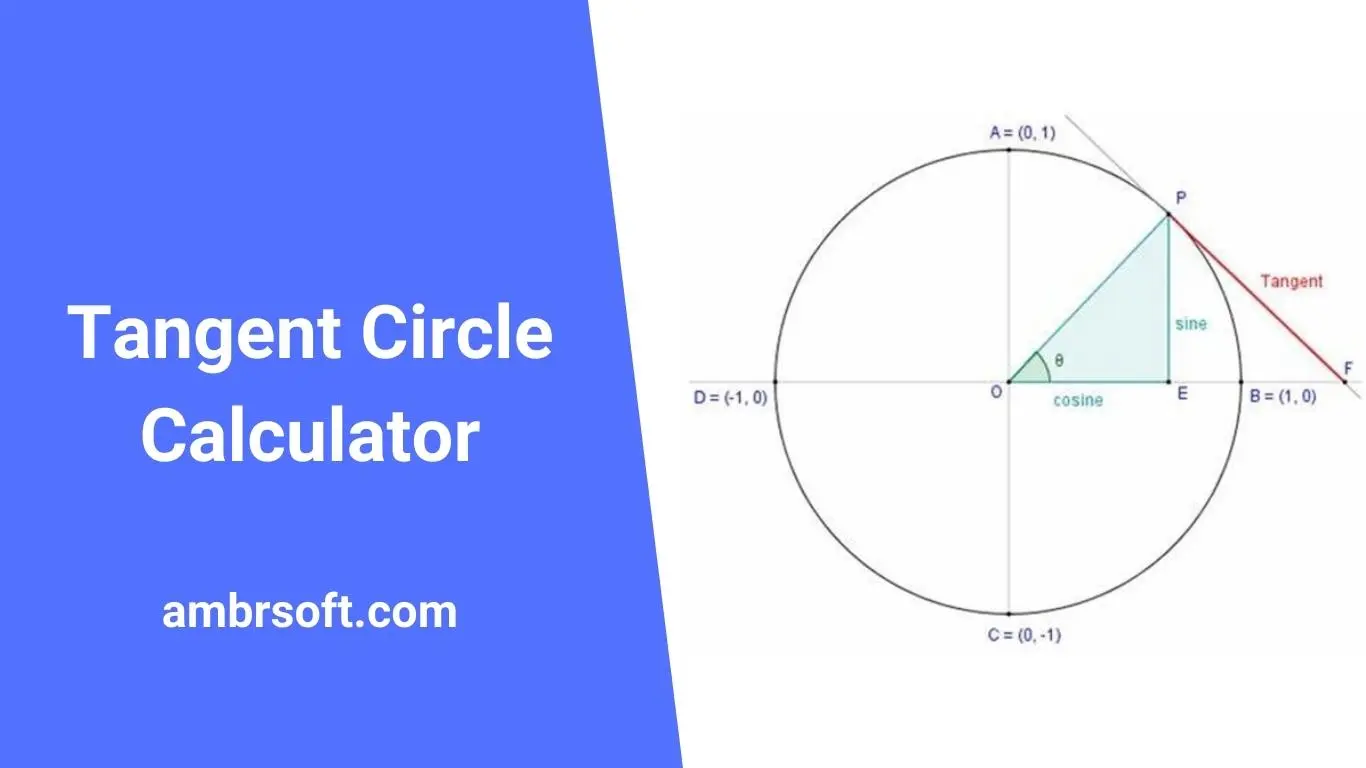
The tangent of an angle is defined as the ratio of two side lengths of the triangle that contains the angle divided by the radius of the circle inscribed in the triangle (or half its perimeter). In order to use a tangent circle calculator, you need to know these three things about your triangle. First, you’ll need to know that all three sides are equal in length and that the angle opposite one of these sides measures 60 degrees (or 1/4 of a circle). Second, you need to know that each side of the triangle lies on either one side or two sides of the inscribed circle.
The problem with finding lengths by other means
is that it can be difficult to know if you’re doing it correctly. A tangent circle calculator will give you the answer directly, so you can be confident that you’re getting the correct result. Plus, it’s easy to use! Just enter the radius of the circle and press ‘calculate’. The length of the tangent will show up in either centimeters or inches.
As always, we hope this helped!
We also hope you’ll share this post with others who might need help with their math problems. It would mean a lot to us to see our posts spread across social media! Sharing is caring, after all.
Calculating the radius
The first step is to find the radius of the circle. You can do this by drawing a line from the center of the circle to the point where the tangent touches the circle. The length of this line is the radius. You can also use a tangent circle calculator to find the radius. Just enter the length of the tangent and it will calculate the radius for you. It’s that easy!
Clear, concise, and informative. When using a tangent circle calculator, make sure to remember to input the length of the tangent. A tangent is the distance between two points on a curve, so if you don’t know the length of the curve you can measure it with a ruler or tape measure. Remember that as long as your measurements are in inches or centimeters then they will work just fine with a tangent circle calculator. Here are some other things to keep in mind when calculating a tangent:
-The equation for calculating the length of the tangent is l=2r*tan(a). Where l is the length of the tangent, r is the radius, and a is the angle subtended at one end by an arc equal in size to 1/2 turn (90 degrees).
Also Check: Air Resistance Calculator
Setting up the problem
A tangent of a circle is a line that touches the circle at only one point. The length of the tangent can be found using the equation: length = radius x tangent. However, this equation only works when you know the value of the tangent. If you don’t know the value of the tangent, you can use a calculator to find it. Here’s how to use a tangent circle calculator to find the length of a tangent.
1) Open up your Tangent Circle Calculator app on your phone or tablet.
2) Input what you know about the problem into the app, which in this case is What is the length of an unknown side?
3) Press enter and solve for unknown side.
4) You will now see three options for solving for unknown side: Calculate Length (length), Calculate Radius (radius), and Calculate Area (area). We want calculate length, so press that option.
Solving for x
In order to solve for x, you’ll need to use a tangent circle calculator. First, identify the radius of the circle. Then, plug that number into the calculator along with the angle at which you wish to find the tangent. The calculator will then give you the length of the tangent. A tangent is always perpendicular to the chord connecting two points on a circle and meets it in exactly one point.
Solving for y
A tangent circle calculator can be used to find the length of a tangent. To use this calculator, you will need the following information: the radius of the circle, and the angle at which the tangent intersects the circle. With this information, you can plug in the values and solve for y. The equation will look something like this: y = r * sin(θ). Once you have solved for y.
Finding the tangent length with equation functions
The first step is to identify the known and unknown variables in the equation. In this case, we know the radius (r) and angle (θ), but we don’t know the length of the tangent (t). Next, we’ll plug in what we know into the equation for a tangent: t = r * tan(θ). Now that we have our equation, we can solve for t by plugging in the values for r and θ. Let’s say r = 3 and θ = 60°. This gives us t = 3 * tan(60°), which simplifies to t = 3 * 1.732, or t = 5.196. This means that the length of the tangent is 5.196 units long.
A few notes on how to approach this type of problem.
When given a circle and asked to find the length of the tangent circle calculator, you will need to use a tangent circle calculator. The first step is to identify the radius of the given circle. The second step is to square the radius. The third step is to multiply the result by 2. The fourth step is to take the square root of the result. The fifth step is to divide the result by 2. The sixth step is to subtract 1 from the result. Finally, take the absolute value of this difference to get your answer.
For example, if the problem was as follows: What is the length of the tangent? Then we would be solving for t. So our equation would be (2)(2)(t) + 1/2 -1 = t^(1/2). Next, we would want to solve for t using the quadratic formula: √((-b ± √((4ac)))/2a). Doing so gives us an answer of 3.988 in decimal form or 12 in fraction form. The final step is to subtract 1 from this number and then take the absolute value of that difference which gives us an answer of 11.