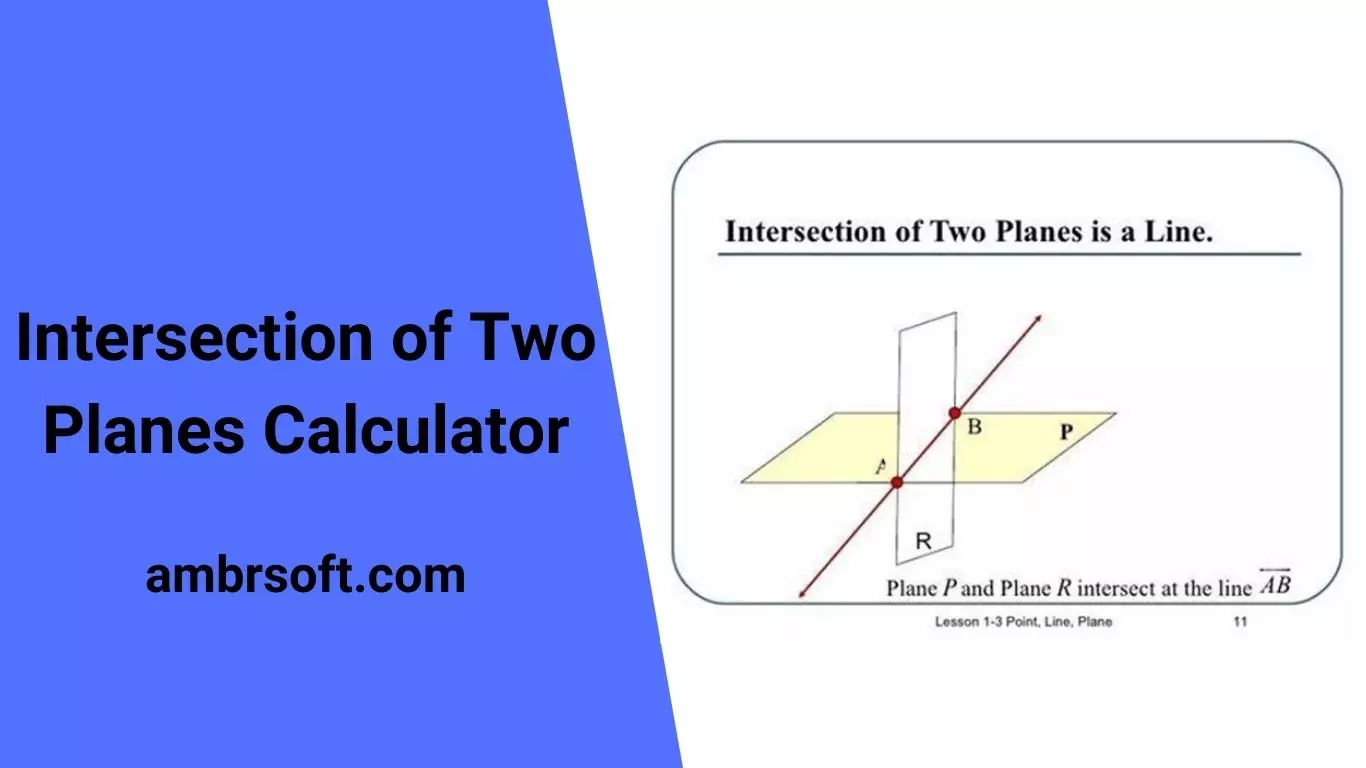
What Is the Intersection of Two Planes Calculator? The intersection of two planes calculator (see attached picture) can be used to find where two planes meet when they are not parallel, but intersect at an angle. What Are Some Uses of the Intersection of Two Planes Calculator? You can use this tool in architecture and engineering to design steel buildings or bridges, as well as wood buildings or furniture that are cut at angles and need to fit together properly without any gaps or overlaps. Where Can I Get the Intersection of Two Planes Calculator?
You can choose from a number of PaydayChampion cash loan choices with immediate approval depending on your need.
About this free online tool
This free online calculator will find the point of Intersection of Two Planes Calculator. Just enter in the plane equation for each plane and hit calculate. The answer will show up in both fraction form and decimal form. This is a great tool for those who are taking geometry or physics class. It can also be used to determine where to place beams, I-beams, or other support structures in order to provide adequate support while maintaining an open floor plan. If you need help understanding this free online calculator, read through our instructions here. There are three basic types of intersecting planes: parallel, skew, and crossing.
Parallel planes do not intersect at all (so there is no solution). Skew intersections produce one solution. Crossing intersections produce two solutions with different coordinates. If we have two lines that intersect but they are neither parallel nor skew then we have crossing planes. In the case of a single line, there will only be one point on that line that crosses another line so there is only one point of intersection. However, if we have two lines that cross then there are two points on either line that can cross another line so there are 2 points of intersection as well as two points along the shared edge between the two lines.
Also Check: Spherical Cap
Writing Equation in Standard Form
In order to calculate the intersection of two planes, you need to write each equation in what is called standard form. Standard form for a plane is Ax + By + Cz = D, where A, B, and C are not all zero. To get an equation in standard form, you can use the following steps:
1) First, determine which variables will have coefficients of 1. These will be your leading terms.
2) Next, choose one of the other variables and write it so that its coefficient is 1. This will be your second term.
3) For the remaining variable, write its coefficient as a negative number.
4) Now, use this equation with the appropriate axis: if the first equation has an x-axis, then put y=0; if the first equation has a y-axis, then put x=0. The numbers on either side of these equal signs represent the axis for which you are solving for values.
5) Solve for one of your coordinates by setting it equal to 0 (keeping in mind that this coordinate is going to appear twice). You should get at least one solution using this method.
How to use the tool
The first step is to input the equation for each plane. You can do this by clicking on the Input Plane 1 and Input Plane 2 buttons. Next, click on the Calculate button. The calculator will then find the point of intersection and display it on the screen. If you want to change either one of the equations, simply edit the equation using the Input Plane 1 or Input Plane 2 buttons before clicking on Calculate again. There are also some things that you should know about the tool:
– When a calculation has been completed, the background color turns from light gray to dark gray.
– When there are an infinite number of points in an equation (for example when a line crosses itself), that result cannot be calculated with this tool.
– To clear your work, click on Clear Results and enter a new set of values for the planes to be intersected.
When might you need it?
You might need to find the Intersection of Two Planes Calculator in many different situations, such as when you’re trying to find the point where two lines intersect or when you’re trying to find the point where a line and a plane intersect. The calculator can be used to help you solve for these types of problems. To use the calculator, simply enter the coefficients of the equations for each plane into the appropriate fields and press calculate. The calculator will then give you the coordinates of the point of intersection. If there is no intersection between the two planes, then an error message will display saying that there is no solution. If you want to clear your input values and start over again, click on Clear Inputs at the bottom of the page.
How to calculate the intersection of two planes?
To calculate the intersection of two planes, you need to find the point of intersection. This can be done by solving a system of linear equations. The first step is to find the normal vectors of both planes. The normal vector is perpendicular to the plane. To find it, you need to take the cross product of any two non-parallel vectors in the plane. Once you have the normal vectors, you can set up the system of linear equations. The next step is to solve for the variables in the system. This will give you the coordinates of the point of intersection. Finally, plug these coordinates into the equation of either plane to verify that they are correct.
Intersection of two lines calculator – with detailed explanation.
The Intersection of Two Planes Calculator. The direction of this line is given by the vector n, which is perpendicular to both planes. To find the point of intersection, we need to find a point that lies on both planes. We can do this by solving a system of linear equations. The first equation comes from plane 1, and the second equation comes from plane 2. We can use any point that lies on either plane as our starting point. For example, let’s use the point (1,2,3) from plane 1 and (0,1,-1) from plane 2. We can plug these points into our equations and solve for x, y, and z.
Other applications
This calculator can also be used to find the point of intersection of two lines in three-dimensional space. To do so, input the coordinates of each line’s two points. The point of intersection will be displayed on the graph. This calculator can also be used to find the point of intersection of a line and a plane in three-dimensional space. To do so, input the coordinates of the line’s point and the plane’s normal vector. The point of intersection will be displayed on the graph.