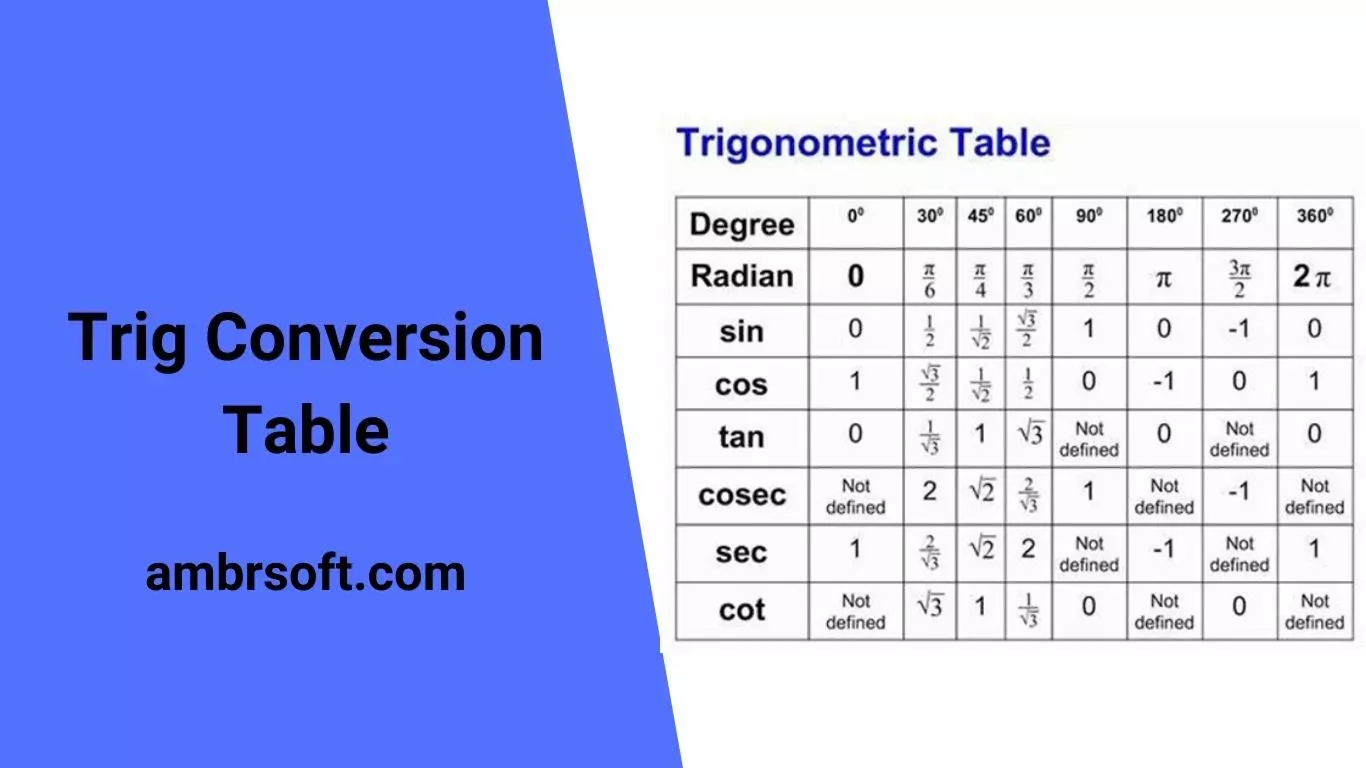
Are you looking for a trig conversion table to help you easily find the measurements you need? If so, you’ve come to the right place! We’ve put together this short guide to all of the most common conversions between different trigonometric functions and their metrics, including sine, cosine, tangent, and more. You don’t have to be an expert in trigonometry to understand this guide, just follow along as we take you through these basics! Let’s get started!
The Basics
If you’re just getting started with trig, you might be feeling a bit overwhelmed. After all, there are so many ratios to remember! But don’t worry, we’re here to help. In this blog post, we’ll provide you with a trig conversion table that will make things a lot easier. Trust us, once you see how easy it is to use this table, you’ll be a pro in no time. So let’s take a look at the basics: First off, there are three types of angles- acute angles (less than 90 degrees), right angles (90 degrees), and obtuse angles (greater than 90 degrees). The numbers within the triangle represent the ratio of the adjacent side over the hypotenuse; while values outside the triangle represent sine and cosine functions. As long as you can remember what those mean, then you’ll be set.
Also Check: Intersection of Two Planes Calculator
How to Convert Radians to Degrees
In trigonometry, a radian is a unit of measurement used to represent angles. One radian is equivalent to 57.29578 degrees. To convert from radians to degrees, simply multiply the number of radians by 57.29578. For example, if you have 2 radians, you would multiply 2 by 57.29578 to get 114.59156 degrees. Alternatively, in order to find out how many degrees are in a radian, divide the degree measurement by 57.29578. For example, if you want to know how many degrees there are in 1 radian, divide 1 by 57.29578 and then multiply that result by 180 degrees. So if you have 1 radian and want to know how many degrees there are in it, take (1/57.29578) * 180 which equals .011727460176961 or about 1 degree. If you need to convert from radians to decimal degrees, use this formula: (degrees*57.29578)/radians. If you need help converting any other units of measurements, check out our complete conversions chart below.
Adding Angles
You can add angles in trig conversion table by finding the sum of their ratios. To do this, you’ll need a trig conversion table. You can find these online or in math textbooks. Once you have the table, simply find the ratios of the angles you’re trying to add and add them together. For example, if you wanted to add 45 degrees and 30 degrees then the ratio is 1:2. If we look at our table, we see that adding 1:2 is equivalent to multiplying 45 degrees by 2 which equals 90 degrees (1 x 2 = 2). So 45+30=90 . In order to subtract angles, you need to find the difference between the two angles being subtracted and then use a negative sign before one of them so it becomes an addition problem. For example, let’s say I want to subtract 35 degrees from 135 degrees. First I would find their difference by taking 135-35=100. Then I would take 100 degrees and apply it as a negative before the right angle since 100 becomes -100 when it’s converted into radians. Now my subtraction problem would be 130-35=-95 but when applied on our conversion table it shows as 130-25=-105 because of how sin(-x) is inverse from sin(x). The last thing we want to know about is multiplying angles together with trigonometry.
Subtracting Angles
To subtract trig conversion table, we simply need to find the difference between the two angles. To do this, we use the formula: Angle 1 – Angle 2 = Angle 3. So, if we want to subtract a 45-degree angle from a 60-degree angle, we would use the following equation: 60 – 45 = 15. This would give us an answer of 15 degrees. We can also add and subtract angles in relation to one another by using the above formula and reversing it. For example, if we wanted to add a 180-degree angle with a 360-degree angle, we would just use the formula 360 + 180 = 540. However, if we want to subtract a 180-degree angle from a 360-degree angle, we would first use the formula 540 – 180 = 360. The trick is that when you subtract any value from 360, you are adding it to 360. So, what would be the answer if we were adding a 180-degree angle with a 1440-degree angle? The simple way is to calculate 1440 – 180 = 1260. However, if you take any number (such as 1440) and divide it by 8 then multiply that number by 10 (1440/8 x 10), you will get exactly what the result should be because 1440 ÷ 8 = 200 x 10= 1200
More About Trig Ratios
trig conversion table is the branch of mathematics that deals with the relationships between the sides and angles of triangles. The most basic ratios in trig are the sine, cosine, and tangent ratios. These ratios are used to find missing sides and angles of triangles. The sine ratio is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine ratio is defined as the ratio of the length of the side adjacent to the angle to the length of hypotenuse. The tangent ratio is defined as the ratio of the length of the side opposite to the angle to the length of the side adjacent to it. The word tangent comes from the Latin word tangere, which means to touch. When dealing with any triangle, it is important to remember that you can only use one trig ratio at a time when solving an equation.
The sine, cosine, and tangent ratios also have corresponding arcsin, arccos, and arctan functions. To calculate a trig conversion table in degrees or radians, multiply its argument by 180/π. To convert degrees to radians, divide by 180/π. To convert radians to degrees, multiply by 180/π. For example: Sin(22°) = Sin(ArcTan (1/2)) = ArcTan (1/2) x 180 / π = 90°.