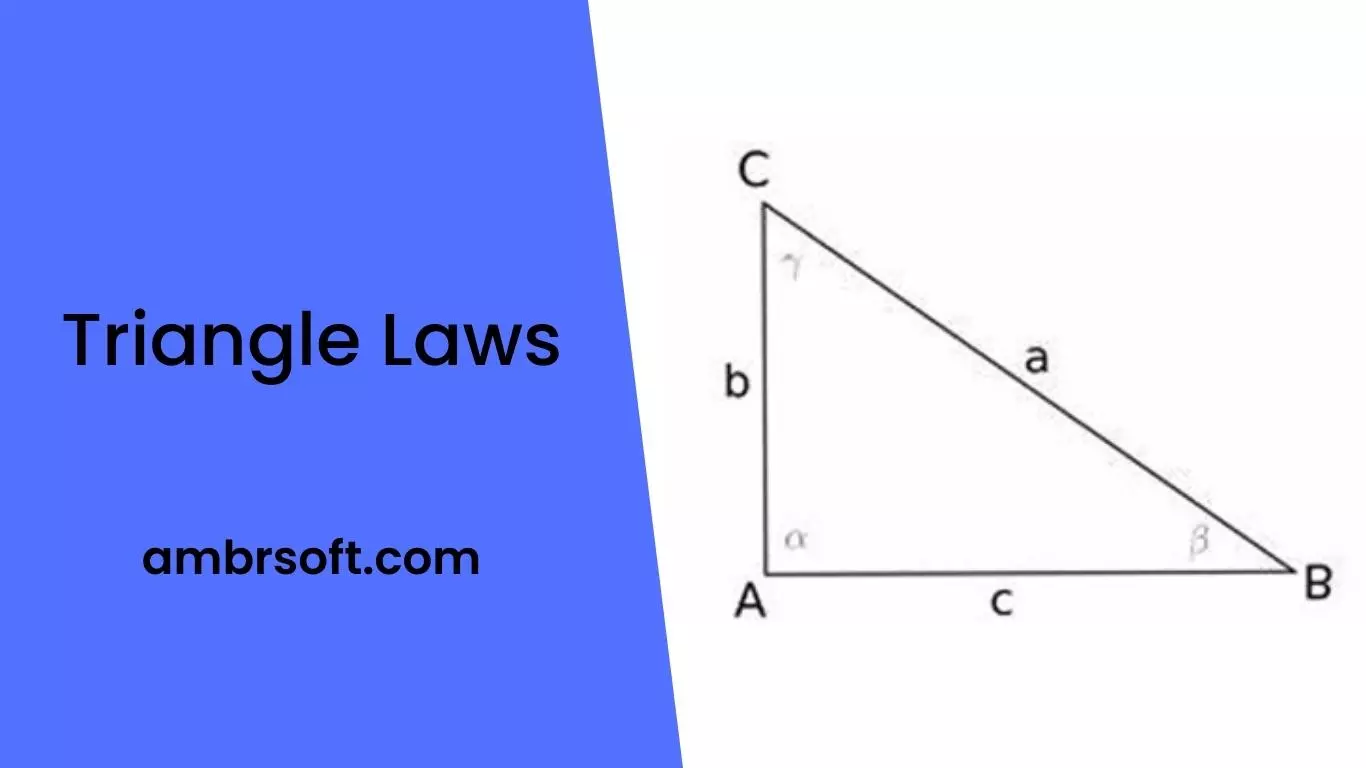
There are three laws that govern the interior angles of any Triangle laws, and knowing these laws can help you solve many different triangle problems that involve trigonometry or geometry. These laws apply to right triangles, acute triangles, obtuse triangles and any other kind of triangle—there’s no getting around them! While there are plenty of rules that come along with these laws, they’re simple enough to understand on your own without memorizing long lists of rules or formulas. Here’s everything you need to know about the interior angles of a triangle.
The Basics
Every triangle has three interior angles, and together they always add up to 180 degrees. This is due to the fact that all the angles on a straight line add up to 180 degrees, and when you put two straight lines together at a point (i.e. form an angle), you’re basically creating a third straight line. So, if you have two interior angles that sum up to 90 degrees, the third one will be 90 degrees as well, and voila! You have a triangle.
There are also some specific Triangle laws that deal with the interior angles: The Sum Rule, The Scalene Triangle Law, and The Isosceles Triangle Law. All three deal with the relationship between different pairs of angles in a triangle. For example, the Scalene Triangle Law states that if two of the angles in a triangle are less than 60 degrees, then their pairwise sums must also be less than 60 degrees. In other words, just because two angles might each be smaller than 60 degrees doesn’t mean their sum will necessarily result in a larger number for the third angle; it’s only true if both angles have a degree measure smaller than 60. The Sum Rule is exactly what it sounds like – it’s about how much one side of any particular angle measures compared to another side.
Also Check: Angle of Inclination Calculator
Side-Angle-Side Formula
The most common way to find the interior angles of a triangle is to use the Side-Angle-Side Formula. This states that the sum of the interior angles of a triangle is equal to 180 degrees. So, if you know two sides and one angle of a triangle, you can find the other two angles. Just remember that all three angles must add up to 180 degrees! There are also some shortcuts you can use to find the interior angles of a triangle quickly: The exterior angle theorem, the Pythagorean Theorem, and Heron’s formula. Some examples include using the exterior angle theorem, which is basically saying that the sum of the measures of the interior angles in any triangle equals 360 degrees. Another useful formula to memorize is the Pythagorean Theorem. It says that for any right triangle with hypotenuse c, c^2 = a^2 + b^2. A more advanced yet still important formula for finding an unknown side or an unknown length within a right triangle has been provided by Heron’s Formula. First, find the measure of the angle opposite what you’re looking for (theta). Next, look at the ratio of lengths from this point on either side of it.
Formulas for Exterior Angle, Hypotenuse, Opposite Side, Adjacent Side and Medians
The exterior angle of a triangle is the angle between any side of the Triangle laws and the extension of its adjacent side. The hypotenuse is the longest side in a right angled triangle and is always opposite to the right angle. The opposite side is the side that is opposite to the given angle in a triangle. The adjacent side is the side that is next to or adjoining something. In geometry, a median of a triangle is a line segment joining a vertex of the triangle to the midpoint of its opposite edge. There are three medians for every triangle. If one of these medians splits the triangle into two equal parts, it is called an altitude, or height. A law of triangles states that if you have three points A, B and C then AB=AC when point B lies on the same side as point A relative to point C.
Multiple Diagonals
A diagonal is a line segment that connects two non-consecutive vertices of a polygon. In other words, it jumps over at least one side. The interior angles of a triangle are the angles inside the triangle that are not on the triangle’s perimeter. The sum of the interior angles of any triangle is always 180 degrees. Since there are three sides and three interior angles, this means each angle equals 60 degrees.
The formula for finding the measure of an exterior angle is subtracting the sum of all interior angles from 360 degrees. There are many ways to find exterior angles in a Triangle laws; you can use Pythagorean Theorem or Cava’s theorem to determine if there is more than one exterior angle in a given triangle. For example, let’s say you have a triangle with the following measurements: 3 units for height, 6 units for length and 5 units for width. Using triangle laws, we know that the length (6) is greater than the height (3). We also know that both of these lengths are greater than the width (5). But what if they were exactly equal? That would mean there would be no exterior angles! The easiest way to solve this problem is using Ceva’s theorem because it uses only parts of triangles which make up its diagram rather than their measurements. If we were able to do so without going off topic too much – which we won’t be able to do because Triangle laws are extensive – then we could use Ceva’s theorem like so
Proof That the Interior Angles Add Up To 180°
We can use algebra to prove that the three interior angles of a triangle always add up to 180°. First, let’s label the three angles. We’ll call them angle A, angle B, and angle C. Now we can create the equation: Angle A + Angle B + Angle C = 180°. We can rearrange this equation to solve for one of the angles: Angle C = 180° – (Angle A + Angle B). So there you have it! The proof that the interior angles of a triangle always add up to 180°. Proof That the Exterior Angles Add up To 360°: In general, exterior angles are larger than their corresponding interior angles. What does this mean? Well, two of the exterior angles in any triangle must sum up to 360° because they total 360 degrees in all-a round measure.
So what about the third exterior angle? That’s easy too-it just equals 180 degrees minus whatever other two exterior angles make up that total 360 degrees between them. Got all that? Let’s try out some examples so you know how to apply these laws. Say your math teacher has drawn an example Triangle laws on the board with all the information labeled appropriately.