If you’ve never heard of the golden ratio equation, also known as the divine proportion, it’s the mathematical relationship between two quantities that creates an aesthetic sense of perfection and balance in any given artwork or design. The golden ratio equation can be used to calculate the value of this ratio in relation to other measurements, so that you can use it to create art or design your own home or office space. For tips on how to use the golden ratio in your own work, keep reading.
What is the Golden Ratio?
You may not know it, but everything in nature has its own set of proportions. Humans are no exception; however, you may not be aware of how many times an object should be divided by another object in order to reach a perfect proportion. These principles have been used for centuries and have a special name: The golden ratio equation. When speaking about geometry and mathematics, the golden ratio is what we call this perfect ratio that creates harmonious designs when applied correctly. This number can be calculated with some pretty simple equations and it applies even if you don’t use this equation as a basic measurement for any creative projects- all you need is knowledge about where it came from!
The Golden Ratio Equation
So how do we calculate the golden ratio? It’s really quite simple! First, find out the length of the long side (L) and divide it by the length of the short side (S). L/S = 1.618… Keep dividing S into L until there’s no more room left. If your answer is 1.618 then congratulations, you’ve just calculated your first golden ratio! If your answer isn’t 1.618, keep dividing S into L until you get to 1.618 again or something close.
Also Read: Kinetic Friction in a Block-and-Pulley System
Golden Ratio Definition
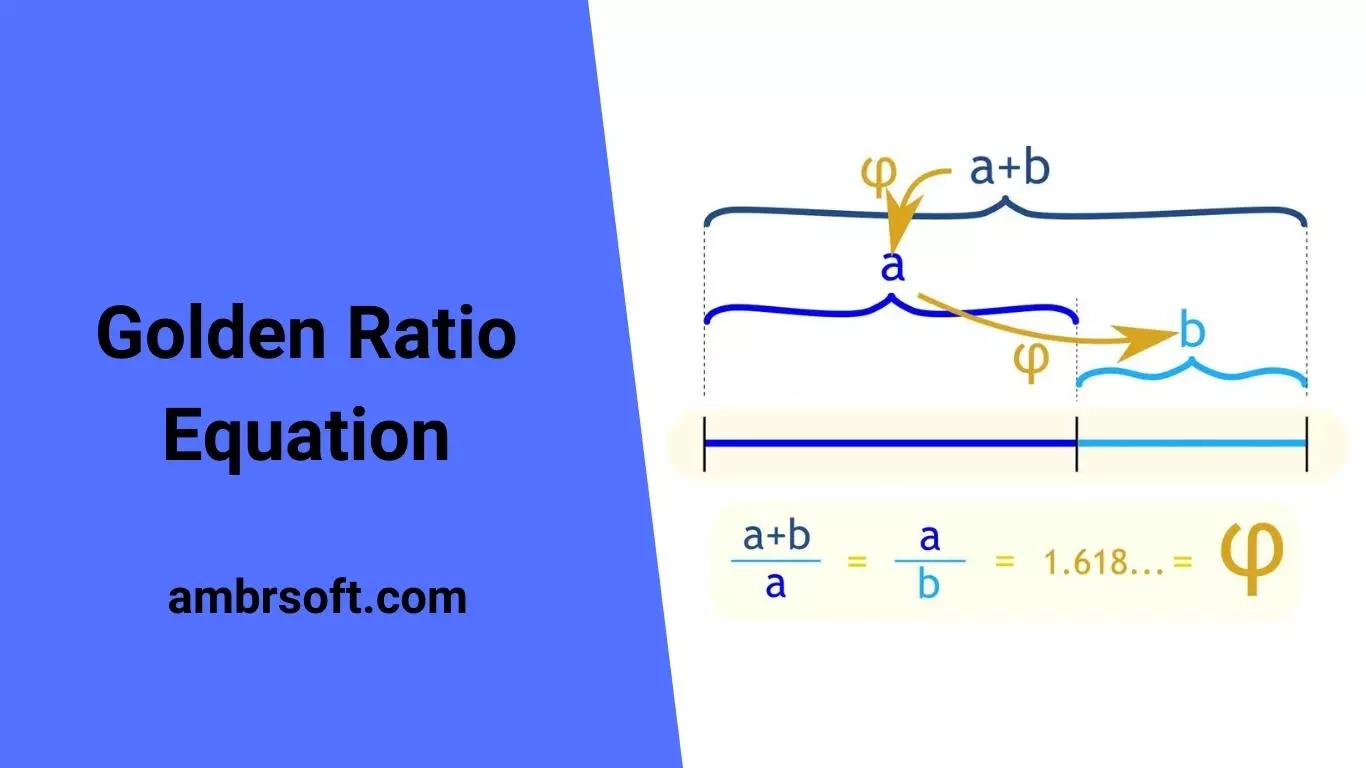
Two sums should be in splendid extent, expecting their extent is comparable to the extent of their total to the greater of the two sums. The splendid extent is around comparable to 1.618. For example, if “a” and “b” are two sums with a>b>0, the splendid extent is logarithmically imparted as follow:
The splendid extent is a senseless number, which is the response for the quadratic condition x2-x-1=0.
for instance Brilliant extent,
Maybe a couple terms that address splendid extent integrate breaking point and mean extent, divine fragment, normal region, splendid cut, and so on.
For example, parcel the line into two fragments. The two fragments are in splendid extent if the extent of the length of the greater section (say, “a”) to the length of the more unassuming portion, (say, “b”) is comparable to the extent of their aggregate “a + b” to the greater region “a” golden ratio equation.
Applications of the Golden Ratio
A formula has been developed that lets us calculate what the perfect golden ratio should be. This formula, based on phi (φ), is shown below: R = φ
Although this equation may seem too complicated for you, it’s actually quite simple. Let’s break it down a little more. R stands for the golden ratio; that is, 1-φ1/φ2. x is a number in a sequence of numbers that are all progressively multiplied by φ until x reaches 1 at φ5. When solving for x in our equation, we use these values from this sequence and find the next one that satisfies the following condition: when multiplied by φ, it gives you a result less than or equal to 1.
Finding the Golden Line
One of the best ways to use a golden ratio equation is in design. For example, if you need a rectangle that’s 4 inches by 6 inches, with 1 inch on each side unclaimed and then have it placed in a square 8 inches by 8 inches, calculate as follows. Make sure you put this equation into parenthesis first though before you start calculating: (1+√5)/2 = 0.814213562374690 (or roughly 82% which is what we want). Next, take √5 and multiply it by 2 to get 1. 61904761904762 or 160%. Now, add both numbers together (82% + 160%) and divide them by two. You’ll find that your ratio should be 81%. Finally, take your final number, 81%, and multiply it by 100 so that you can make it easier to do calculations with decimal points. Your final answer will be 8.1045454545548 or 81⁄2 inches long.
Golden Ratio Value Derivation
Take any line segment and let it be AB. Put A on one end of a longer line segment, BC, and B on the other end. Then draw a smaller line segment AC that is equal in length to AB and put C at one end of that shorter line segment, DC. Where AC meets BC, mark where E is on BC with a cross-mark so that you can see it. Draw another line down from E till it intersects with AC, which will give you FG. Next mark H on DC somewhere near F. Now measure FH. The distance is the same as AE – but rotated 180 degrees around AC! That means HJ is also equal to AE! So why don’t we just measure it golden ratio equation?
Practice Question
1. Which of the going with address the splendid extent condition?
a/b = (a+b)/b
a/b = (a+b)/a
a/b = (a-b)/b
a/b = (a-b)/a
2. The splendid extent ϕ is comparable to
ϕ – 1
ϕ + 1
1 + (1/ϕ)
1 – (1/ϕ)
To learn more Math’s-related thoughts successfully golden ratio equation, – The Learning App, and explore many captivating accounts.
Frequently Asked Questions about Golden Ratio
What is the brilliant proportion?
In Mathematics, two amounts are supposed to be in brilliant proportion, assuming that their proportion is equivalent to the proportion of their aggregate to the bigger of the two amounts.
Which image is utilized to address the brilliant proportion?
The image used to address brilliant proportion is ϕ (phi).
What is the worth of the brilliant proportion?
The worth of the brilliant proportion is around equivalent to 1.618.
How is the brilliant proportion connected with the Fibonacci grouping?
There exists a connection between the brilliant proportion and Fibonacci grouping, to such an extent that the proportion of two progressive terms in the Fibonacci succession is extremely nears the brilliant proportion.